Welcome to Deutsche Telekom’s innovation
program on Artificial Intelligence.
We love ai
Join our next ONLINE EVENT on September 29

36
days
23
hours
12
minutes
44
seconds


What we are working on
Story
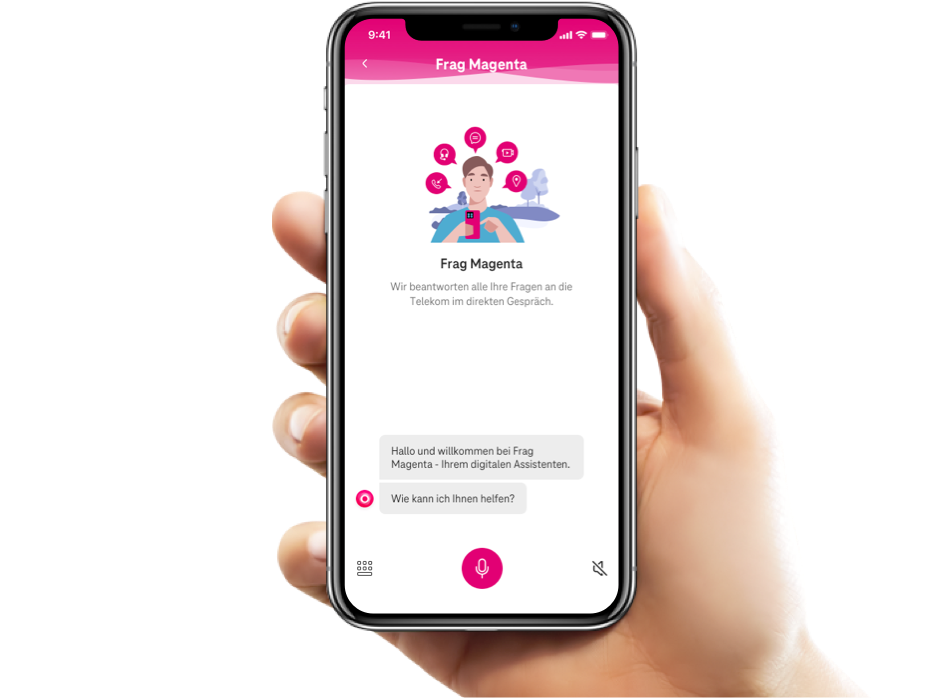
Frag Magenta
We have built and are constantly improving support for our customers with our digital assistant. Human-like, easy-to-access, no-waiting, around-the-clock.

Story
eMpathic
We are buiding Deutsche Telekoms' ‘connected brain’ that individualises customer interactions across all touchpoints and the customer lifecycle.



